Approximating Differential Equations

Here’s how to approximate a differential equation using discrete simulations in R. Differential equations will be presented in the form

dxdt

where dx is the change in whatever stock x represents and dt is the length of the time step. Any differential equation can be rearranged as

dx=f()∗dt.

where some function is multiplied by the time step dt. In R, you could make this time step 0.000001, which is close enough to continuous that it often approximates functions well. Once you calculate dx, or the change in x over a small time step (i.e., 0.000001), then you can add this change to the current value of x:

xnew=x+dx

Rinse and repeat. Here is an example using the famous Lotka-Volterra Equations. Predator-Prey dynamics can be modeled with:

dxdt=Ax−Bxy

dydt=Cxy−Dy

where

• x is the number of prey
• y is the number of predators
• A is the birth rate of prey
• B is the contact rate between predators and prey
• C can either be equivalent to B, or it can be thought of as the predator birth rate due to the presence of prey
• D is the death rate of predators in the absence of prey
• dx is the change in number of prey
• dy is the change in the number of predators
• dt is the time step (not number of time points).

We can numerically approximate these equations by multiplying each equation by dt and then simulating with a small time step (e.g., 0.0001).

A discrete time version would be:

dx <- (Ax - Bxy) * small_step
dy <- (Cxy - Dy) * small_step

x_new <- x + dx
y_new <- y + dy

repeat many times...

Let’s run it.

step <- 0.1
time <- seq(from = step, to = 100, by = step)
x <- numeric(length(time))
y <- numeric(length(time))
x[1] <- 3
y[1] <- 5
A <- 1
B <- 0.2
C <- 0.04
D <- 0.5

count <- 0
for(i in time){
  count <- count + 1
  
  
  dx <- (A*x[count] - B*x[count]*y[count]) * step
  dy <- (C*x[count]*y[count] - D*y[count]) * step
  
  x_new <- x[count] + dx
  y_new <- y[count] + dy
  
  x[count + 1] <- x_new
  y[count + 1] <- y_new
  
  
}

library(tidyverse)
library(ggplot2)
library(hrbrthemes)

df <- data.frame(
  'time' = c(time, time),
  'val' = c(x[1:length(time)], y[1:length(time)]),
  'var' = c(rep("Prey", length(time)),
            rep("Predator", length(time)))
)


ggplot(df, aes(x = time, y = val, color = var)) + 
  geom_line() + 
  theme_ipsum()

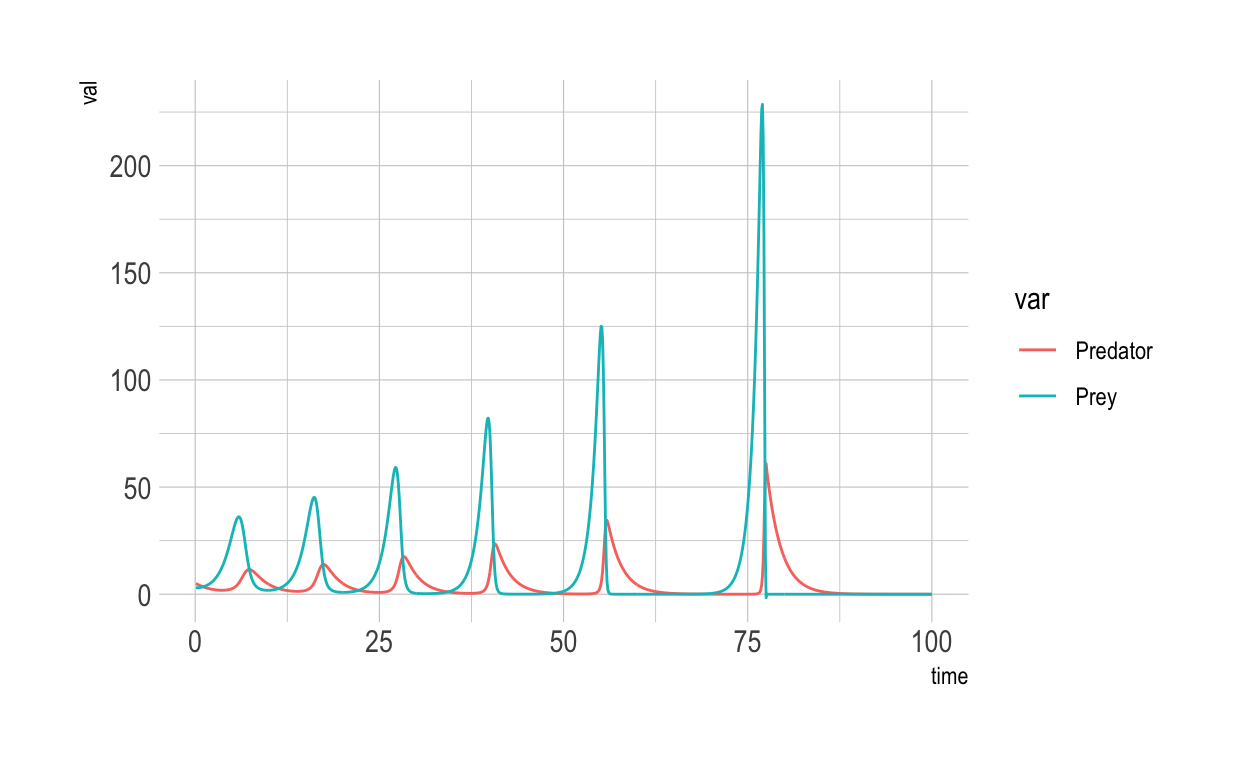
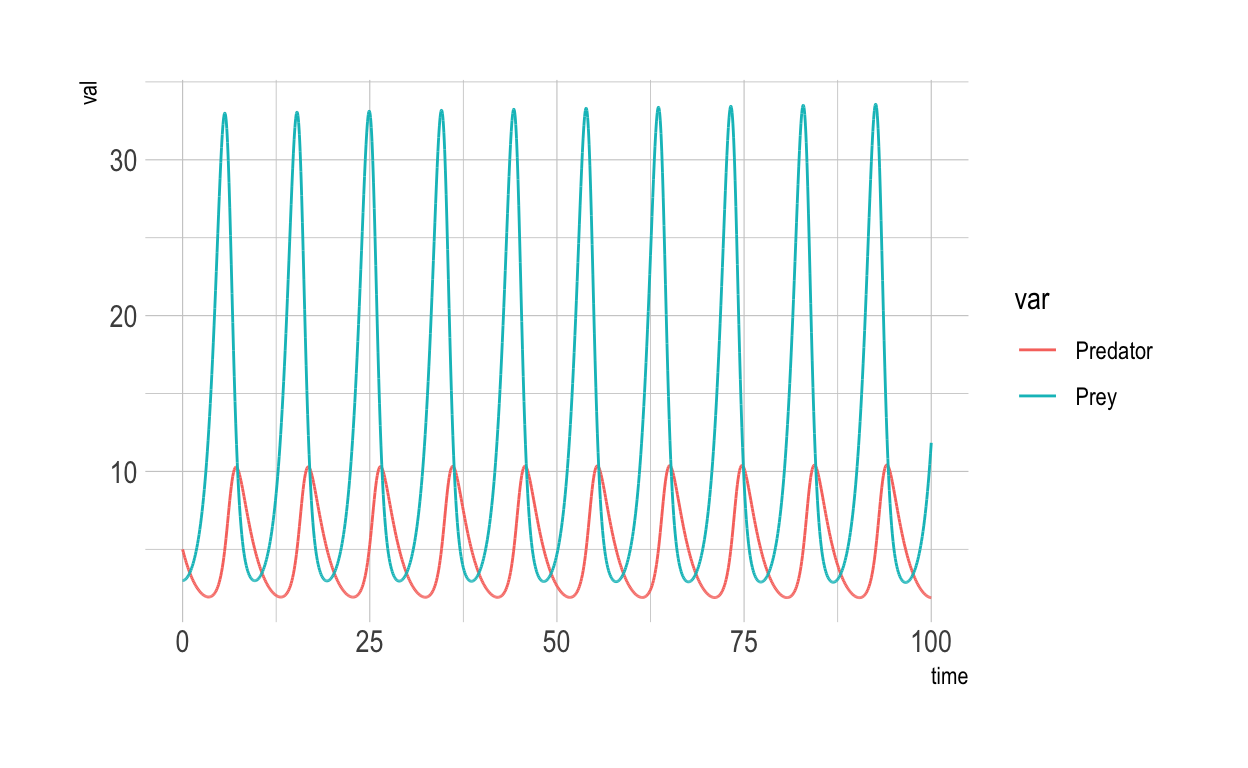
Cool. The ever-growing size of the spikes is an artifact of approximation. Let’s use an even smaller step:

step <- 0.001

Here is the output:

In these simulations, I used what I call a “push forward” approach (i.e., generate x at t + 1 from x current). Sometimes, I prefer to use a “look backward” approach (i.e., generate x from x at t - 1). Here is the second approach:

step <- 0.001
time <- 1000
x <- numeric(length(time))
y <- numeric(length(time))
x[1] <- 3
y[1] <- 5
A <- 1
B <- 0.2
C <- 0.04
D <- 0.5

for(i in 2:time){

  
  dx <- (A*x[i - 1] - B*x[i - 1]*y[i - 1]) * step
  dy <- (C*x[i - 1]*y[i - 1] - D*y[i - 1]) * step
  
  x_new <- x[i - 1] + dx
  y_new <- y[i - 1] + dy
  
  x[i] <- x_new
  y[i] <- y_new
  
  
}

Bo2m =)